安全和密码学

开课注解

本节与版本控制（Git）在同一节线下课讲授

介绍

去年的这节课我们从计算机 用户 的角度探讨了增强隐私保护和安全的方法。 今年我们将关注比如散列函数、密钥生成函数、对称/非对称密码体系这些安全和密码学的概念是如何应用于前几节课所学到的工具（Git和SSH）中的。

本课程不能作为计算机系统安全 (6.858) 或者 密码学 (6.857以及6.875)的替代。 如果你不是密码学的专家，请不要试图创造或者修改加密算法。从事和计算机系统安全相关的工作同理。

这节课将对一些基本的概念进行简单（但实用）的说明。 虽然这些说明不足以让你学会如何 设计 安全系统或者加密协议，但我们希望你可以对现在使用的程序和协议有一个大概了解。

熵

熵(Entropy) 度量了不确定性并可以用来决定密码的强度。

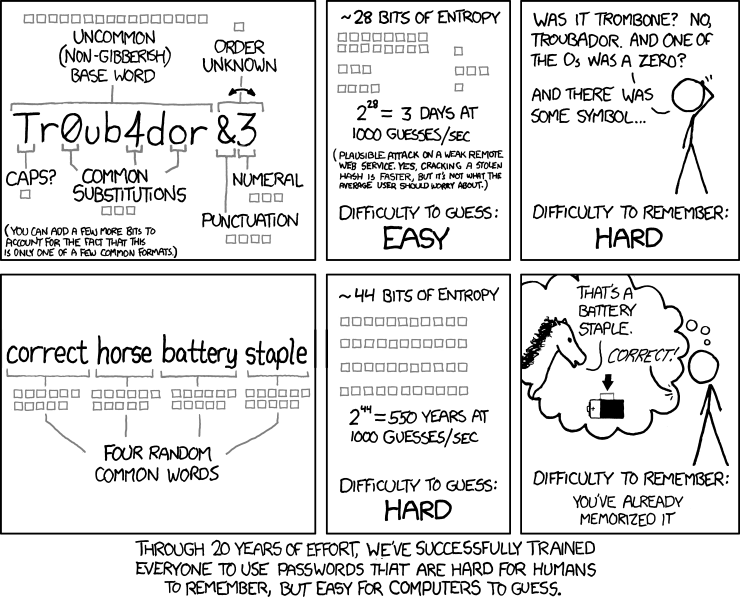
XKCD 936: Password Strength

正如上面的 XKCD 漫画 所描述的， “correcthorsebatterystaple” 这个密码比 “Tr0ub4dor&3” 更安全——可是熵是如何量化安全性的呢？

熵的单位是 比特。对于一个均匀分布的随机离散变量，熵等于log_2(所有可能的个数，即n)。 扔一次硬币的熵是1比特。掷一次（六面）骰子的熵大约为2.58比特。

一般我们认为攻击者了解密码的模型（最小长度，最大长度，可能包含的字符种类等），但是不了解某个密码是如何随机选择的—— 比如掷骰子。

使用多少比特的熵取决于应用的威胁模型。 上面的XKCD漫画告诉我们，大约40比特的熵足以对抗在线穷举攻击（受限于网络速度和应用认证机制）。 而对于离线穷举攻击（主要受限于计算速度）, 一般需要更强的密码 (比如80比特或更多)。

散列函数

密码散列函数 (Cryptographic hash function) 可以将任意大小的数据映射为一个固定大小的输出。除此之外，还有一些其他特性。 一个散列函数的大概规范如下：

hash(value: array<byte>) -> vector<byte, N>  (N对于该函数固定)

SHA-1是Git中使用的一种散列函数， 它可以将任意大小的输入映射为一个160比特（可被40位十六进制数表示）的输出。 下面我们用sha1sum命令来测试SHA1对几个字符串的输出：

$ printf 'hello' | sha1sum
aaf4c61ddcc5e8a2dabede0f3b482cd9aea9434d
$ printf 'hello' | sha1sum
aaf4c61ddcc5e8a2dabede0f3b482cd9aea9434d
$ printf 'Hello' | sha1sum 
f7ff9e8b7bb2e09b70935a5d785e0cc5d9d0abf0

抽象地讲，散列函数可以被认为是一个不可逆，且看上去随机（但具确定性）的函数 （这就是散列函数的理想模型）。 一个散列函数拥有以下特性：

注：虽然SHA-1还可以用于特定用途，但它已经不再被认为是一个强密码散列函数。 你可参照密码散列函数的生命周期这个表格了解一些散列函数是何时被发现弱点及破解的。 请注意，针对应用推荐特定的散列函数超出了本课程内容的范畴。 如果选择散列函数对于你的工作非常重要，请先系统学习信息安全及密码学。

密码散列函数的应用

密钥生成函数

密钥生成函数 (Key Derivation Functions) 作为密码散列函数的相关概念，被应用于包括生成固定长度，可以使用在其他密码算法中的密钥等方面。 为了对抗穷举法攻击，密钥生成函数通常较慢。

密钥生成函数的应用

对称加密

说到加密，可能你会首先想到隐藏明文信息。对称加密使用以下几个方法来实现这个功能：

keygen() -> key  (这是一个随机方法)

encrypt(plaintext: array<byte>, key) -> array<byte>  (输出密文)
decrypt(ciphertext: array<byte>, key) -> array<byte>  (输出明文)

加密方法encrypt()输出的密文ciphertext很难在不知道key的情况下得出明文plaintext。
解密方法decrypt()有明显的正确性。因为功能要求给定密文及其密钥，解密方法必须输出明文：decrypt(encrypt(m, k), k) = m。

AES 是现在常用的一种对称加密系统。

对称加密的应用

非对称加密

非对称加密的“非对称”代表在其环境中，使用两个具有不同功能的密钥： 一个是私钥(private key)，不向外公布；另一个是公钥(public key)，公布公钥不像公布对称加密的共享密钥那样可能影响加密体系的安全性。
非对称加密使用以下几个方法来实现加密/解密(encrypt/decrypt)，以及签名/验证(sign/verify)：

keygen() -> (public key, private key)  (这是一个随机方法)

encrypt(plaintext: array<byte>, public key) -> array<byte>  (输出密文)
decrypt(ciphertext: array<byte>, private key) -> array<byte>  (输出明文)

sign(message: array<byte>, private key) -> array<byte>  (生成签名)
verify(message: array<byte>, signature: array<byte>, public key) -> bool  (验证签名是否是由和这个公钥相关的私钥生成的)

非对称的加密/解密方法和对称的加密/解密方法有类似的特征。
信息在非对称加密中使用 公钥 加密， 且输出的密文很难在不知道 私钥 的情况下得出明文。
解密方法decrypt()有明显的正确性。 给定密文及私钥，解密方法一定会输出明文： decrypt(encrypt(m, public key), private key) = m。

对称加密和非对称加密可以类比为机械锁。 对称加密就好比一个防盗门：只要是有钥匙的人都可以开门或者锁门。 非对称加密好比一个可以拿下来的挂锁。你可以把打开状态的挂锁（公钥）给任何一个人并保留唯一的钥匙（私钥）。这样他们将给你的信息装进盒子里并用这个挂锁锁上以后，只有你可以用保留的钥匙开锁。

签名/验证方法具有和书面签名类似的特征。
在不知道 私钥 的情况下，不管需要签名的信息为何，很难计算出一个可以使 verify(message, signature, public key) 返回为真的签名。
对于使用私钥签名的信息，验证方法验证和私钥相对应的公钥时一定返回为真： verify(message, sign(message, private key), public key) = true。

非对称加密的应用

密钥分发

非对称加密面对的主要挑战是，如何分发公钥并对应现实世界中存在的人或组织。

Signal的信任模型是，信任用户第一次使用时给出的身份(trust on first use)，同时支持用户线下(out-of-band)、面对面交换公钥（Signal里的safety number）。

PGP使用的是信任网络。简单来说，如果我想加入一个信任网络，则必须让已经在信任网络中的成员对我进行线下验证，比如对比证件。验证无误后，信任网络的成员使用私钥对我的公钥进行签名。这样我就成为了信任网络的一部分。只要我使用签名过的公钥所对应的私钥就可以证明“我是我”。

Keybase主要使用社交网络证明 (social proof)，和一些别的精巧设计。

每个信任模型有它们各自的优点：我们（讲师）更倾向于 Keybase 使用的模型。

案例分析

密码管理器

每个人都应该尝试使用密码管理器，比如KeePassXC、pass 和 1Password)。

密码管理器会帮助你对每个网站生成随机且复杂（表现为高熵）的密码，并使用你指定的主密码配合密钥生成函数来对称加密它们。

你只需要记住一个复杂的主密码，密码管理器就可以生成很多复杂度高且不会重复使用的密码。密码管理器通过这种方式降低密码被猜出的可能，并减少网站信息泄露后对其他网站密码的威胁。

两步验证（双因子验证）

两步验证(2FA)要求用户同时使用密码（“你知道的信息”）和一个身份验证器（“你拥有的物品”，比如YubiKey）来消除密码泄露或者钓鱼攻击的威胁。

全盘加密

对笔记本电脑的硬盘进行全盘加密是防止因设备丢失而信息泄露的简单且有效方法。 Linux的cryptsetup + LUKS， Windows的BitLocker，或者macOS的FileVault都使用一个由密码保护的对称密钥来加密盘上的所有信息。

聊天加密

Signal和Keybase使用非对称加密对用户提供端到端(End-to-end)安全性。

获取联系人的公钥非常关键。为了保证安全性，应使用线下方式验证Signal或者Keybase的用户公钥，或者信任Keybase用户提供的社交网络证明。

SSH

我们在之前的一堂课讨论了SSH和SSH密钥的使用。那么我们今天从密码学的角度来分析一下它们。

当你运行ssh-keygen命令，它会生成一个非对称密钥对：公钥和私钥(public_key, private_key)。 生成过程中使用的随机数由系统提供的熵决定。这些熵可以来源于硬件事件(hardware events)等。 公钥最终会被分发，它可以直接明文存储。 但是为了防止泄露，私钥必须加密存储。ssh-keygen命令会提示用户输入一个密码，并将它输入密钥生成函数 产生一个密钥。最终，ssh-keygen使用对称加密算法和这个密钥加密私钥。

在实际运用中，当服务器已知用户的公钥（存储在.ssh/authorized_keys文件中，一般在用户HOME目录下），尝试连接的客户端可以使用非对称签名来证明用户的身份——这便是挑战应答方式。 简单来说，服务器选择一个随机数字发送给客户端。客户端使用用户私钥对这个数字信息签名后返回服务器。 服务器随后使用.ssh/authorized_keys文件中存储的用户公钥来验证返回的信息是否由所对应的私钥所签名。这种验证方式可以有效证明试图登录的用户持有所需的私钥。

资源

课后练习

原习题解答

  1. 熵
    1. 假设一个密码是由四个小写的单词拼接组成，每个单词都是从一个含有10万单词的字典中随机选择，且每个单词选中的概率相同。 一个符合这样构造的例子是correcthorsebatterystaple。这个密码有多少比特的熵？
    2. 假设另一个密码是用八个随机的大小写字母或数字组成。一个符合这样构造的例子是rg8Ql34g。这个密码又有多少比特的熵？
    3. 哪一个密码更强？
    4. 假设一个攻击者每秒可以尝试1万个密码，这个攻击者需要多久可以分别破解上述两个密码？
  2. 「加分」密码散列函数 从Debian镜像站下载一个光盘映像（也可以使用你之前下载的Ubuntu的镜像）。使用sha256sum命令对比下载映像的哈希值和官方Debian站公布的哈希值。如果你下载了上面的映像，官方公布的哈希值可以参考这个文件（对于Ubuntu来说大部分镜像站的下载目录中都会包含哈希文件及其签名）。
  3. 对称加密 使用 OpenSSL的AES模式加密一个文件: openssl aes-256-cbc -salt -in {源文件名} -out {加密文件名}。 使用cat或者hexdump对比源文件和加密的文件，再用 openssl aes-256-cbc -d -in {加密文件名} -out {解密文件名} 命令解密刚刚加密的文件。最后使用cmp命令确认源文件和解密后的文件内容相同。
  4. 「加分」非对称加密
    1. 在你自己的电脑上使用更安全的ED25519算法生成一组SSH 密钥对。为了确保私钥不使用时的安全，一定使用密码加密你的私钥。
    2. 配置GPG。
    3. 使用git commit -S命令签名一个Git提交，并使用git show --show-signature命令验证这个提交的签名。或者，使用git tag -s命令签名一个Git标签，并使用git tag -v命令验证标签的签名。（提示：在本地操作即可）

Edit this page.

Licensed under CC BY-NC-SA.